上一期的AMC8真題主要考察了一次方程、排列組合、求立體(ti) 幾何麵積等知識哦。
來看看本期老師帶來的答案解析吧!
第1題
A bus takes 2 minutes to drive from one stop to the next, and waits 1 minute at each stop to letpassengers board. Zia takes 5 minutes to walk from one bus stop to the next. As Zia reaches a busstop, if the bus is at the previous stop or has already left the previous stop, then she will wait for thebus. Otherwise she will start walking toward the next stop. Suppose the bus and Zia start at the same time toward the library, with the bus stops 3 behind. After how many minutes will Zia board the bus?
一輛公共汽車從(cong) 一個(ge) 站開到下一個(ge) 站需要 2 分鍾,在每個(ge) 站乘客上下車需要等待 1 分鍾。Zia從(cong) 一個(ge) 公共汽車站走到下一個(ge) 站需要 5 分鍾。當 Zia 到達一個(ge) 公共汽車站時,如果公共汽車是在上一站或已經離開上一站,那麽(me) 她會(hui) 等待公共汽車。否則,她將走向下一站。假設公共汽車和 Zia 同時出發前往圖書(shu) 館,公共汽車落後 3 站。問多少分鍾以後,Zia 將登上公共汽車?
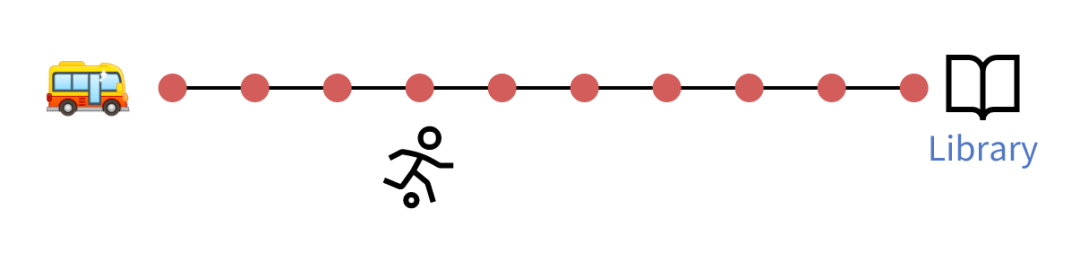
這道題可以通過列方程式求出答案。
解題關(guan) 鍵在於(yu) 理解題目中的數量關(guan) 係。
根據題目,我們(men) 知道如果汽車在上一站或剛離開上一站,Zia會(hui) 選擇等待。
公交車每分鍾經過1/(2+1)站,也就是1/3站;Zia每分鍾經過1/5站。
設x分鍾時,公交車到達或剛離開Zia的上一站,根據關(guan) 係列出等式:
1/3x=1/5x+3-1
x=15
所以Zia還要再等2分鍾才坐上汽車,也就是15+2=17分鍾。
第2題
A ∆or ◯ is placed in each of the nine squares in a 3-by-3 grid. Shown below is a sample configuration with three ∆s in a line. How many configurations will have three ∆s in a line and three ◯s in a line? 在 3×3 方格表的九個(ge) 單元格的每個(ge) 中放置∆或◯。下圖是一種有三個(ge) ∆在一條線上的放置方法。問在有三個(ge) ∆在一條線上,並且有三個(ge) ◯在一條線上的放置方法有多少種?
本題考察排列組合的相關(guan) 知識。
如果要保證三個(ge) ∆和三個(ge) ◯都在一條直線上,那麽(me) ∆或◯都不可能走斜線,隻能走直線。
那麽(me) 可以推出下麵2種可能的情況:
∆占兩(liang) 條線,◯占一條線;或者反之。
可以得到3!/2=(3×2×1)/2=6/2=3
占一條線的可能性有兩(liang) 種,無非是∆或◯,
所以3×2=6。
∆占一條線,◯占一條線,第三條線二者隨機排列。
排列方法有3!=6種,
一共有2³-2=6種方法排列第三條線,
同時要減去2,防止和情況1第三條線都是∆或◯的情況重合。
可以得到6×6=36,
所以最終總數為(wei) 2(6+36)=2×42=84。
第3題
The figure below shows a polygon ABCDEFGH, consisting of rectangles and right triangles.When cut out and folded on the dotted lines, the polygon forms a triangular prism. Suppose that AH=EF=8 and GH=14. What is the volume of the prism? 下圖所示的多邊形 ABCDEFGH 由長方形和直角三角形組成。當把它剪出並沿虛線折疊後,該多邊形可以形成一個(ge) 底麵是三角形的棱柱。假設 AH=EF=8,GH=14。問該棱柱的體(ti) 積是多少?

這道題很考察同學們(men) 的空間想象力,這方麵薄弱的同學要多練習(xi) 相似的題目哦!
求棱柱的體(ti) 積,我們(men) 需要用到公式:
S=底麵積×高
根據題目,已知AH=EF=8,GH=14,而且棱柱的底麵是直角三角形,
那麽(me) 如果BJG為(wei) 底麵,我們(men) 可以畫出這個(ge) 棱柱的折疊圖,如下:
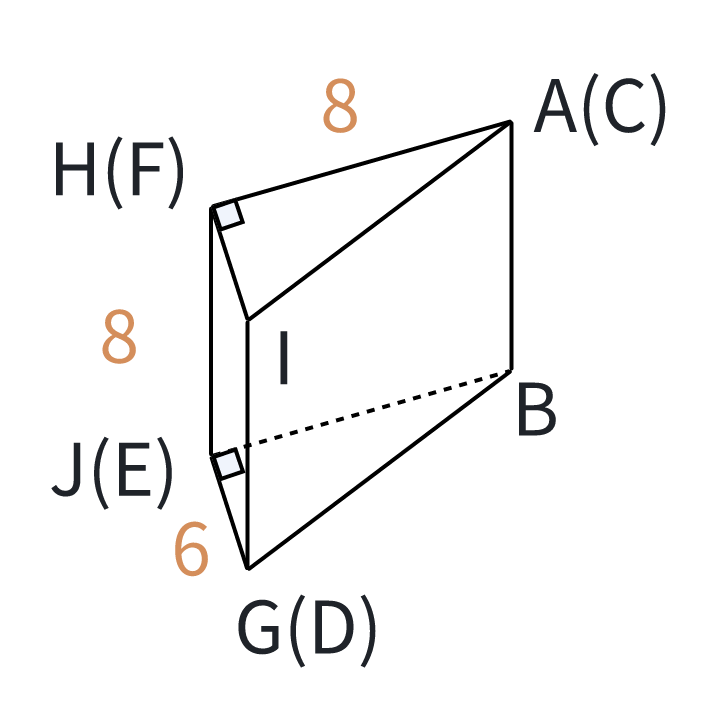
因為(wei) 三角形AHI全等於(yu) 三角形BJG,
所以BJ=AH=8,
又因為(wei) ∠BJG=90°,
所以該直角三角形麵積可求
即SBJG=6×8×1/2=24
棱柱的高為(wei) HJ=8
所以棱柱的麵積S=24×8=192。
解題tips:
立體(ti) 幾何解題,空間感很重要,不擅長的同學要多鍛煉哦。














評論已經被關(guan) 閉。